신경망에서 학습을 시킨다는 의미

신경망에서는 데이터 간의 연관 관계를 기억하는 능력을 가지고 있고, 데이터로부터 연관관계를 표현할 수 있는 특정한 수식을 자동으로 찾아내는 동작을 수행합니다.

그러면 어떤 동작을 수행하기에 신경망에서는 자동으로 수식을 찾아낼 수 있는 걸까요. 바꿔 말해 신경망은 어떻게 학습을 수행하는 것일까요. 해당 글에서는 신경망의 학습이라는 주제로 해당 궁금증을 해결해보도록 하겠습니다.

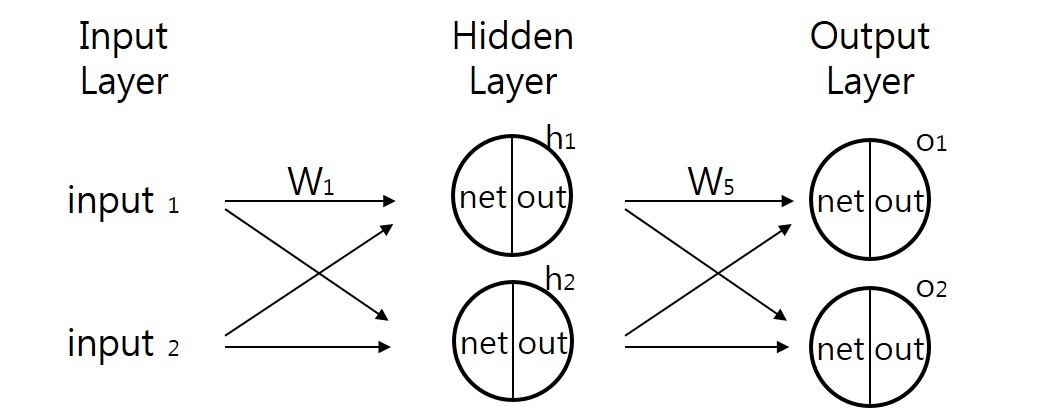
해당 그림은 간단한 형태의 뉴럴 네트워크입니다.

뉴럴 네트워크는 가장 왼쪽에 입력 데이터가 들어오면, 가장 오른쪽에 출력 데이터를 내보내게 됩니다. 그 사이에는 다양한 선들과 동그라미가 보입니다.

이떄 선들은 각자 고유한 값을 가지게 되며, 선들은 자신의 왼쪽 동그라미의 값과 자신이 가진 값을 곲아여 오른쪽 동그라미로 넘겨줍니다. 동그라미는 이때 들어오는 모든 값을 더해 자신의 값으로 두게 됩니다. 그리고 더한 값이 0보다 크면 오른쪽으로 내보내고 0보다 작으면 아무것도 하지 않습니다.

또한 첫 번째로 제시된 그림을 살펴보면 아래 x 축 쯔음에 layer라는 글씨가 연속적으로 보일 것입니다. 신경망은 이러한 layer의 연속으로 구성됩니다. 모든 layer를 함께 보면 복잡해보이지만 일부만 따로 떼어서 보면 다음과 같습니다.

1th 동그라미 x 0.1 + 2th 동그라미 x 0.2 + 3th 동그라미 x 0.5 와 같은 형태로 표현이 가능합니다.

이러한 구조를 통해 뉴럴 네트워크에 존재하는 선들이 어떤 수식을 구성하는데에 사용됩니다. 선들의 값이 바뀌면 뉴럴 네트워크가 표현하는 수식 또한 바뀌게 됩니다.

즉 뉴럴 네트워크 학습의 핵심은 선들의 값을 잘 찾아내는 것이라고 할 수 있겠습니다.

올바른 선들의 값을 찾아낸다면, 연관관계를 잘 표현하는 수식을 만들어낼 수 있게 되고, 결국 연관관계를 잘 기억해내는 잘 학습된 뉴럴 네트워크가 완성되는 것입니다. 이때 선의 값을 가중치(Weight)라는 용어로 부르게 됩니다.

그런데 적절한 가중치를 찾는 것은 상당히 어려운 문제입니다. 최신 뉴럴 네트워크에서는 이러한 가중치 값들을 수천만개 많게는 수천억개 이상을 가지고 있습니다. 어떻게 적절한 가중치 값들을 찾을 수 있을까요?

수십년 동안 많은 방법들이 제시되어 왔지만, 그 중 상당히 많이 사용되는 역전파 알고리즘에 대해서 설명하고자 합니다.

학습에 앞서 다음과 같은 데이터셋이 있다고 가정해봅시다. 우리는 강아지와 고양이를 분류해야 합니다. 앞서 제시된 데이터에서는 해당 데이터가 어떤 동물인지에 대해서 애노테이션(라벨이라고도 불림)을 갖고 있습니다.

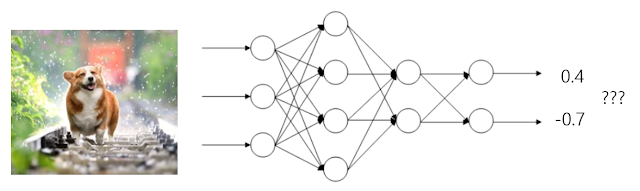
신경망 학습 이전에는 이미지를 넣어도 예측을 정상적으로 할 수 없겠죠. 강아지 이미지를 넣으면 (1, 0)의 값이 나오는 것이 이상적이지만 지금은 (0.4, -0.7)의 잘못된 값이 나옵니다. 이를 개선하여 (1, 0)의 값이 나올 수 있도록 개선해야 합니다.

조금 바꿔말하면 목표(데이터셋)와 현상태(현재 네트워크의 동작)의 차이를 최소화 하는 방향으로 선의 값을 변경해야 합니다. 현재 차이를 계산해보면 (0.6, 0.7)만큼의 괴리가 발생함을 알 수 있습니다.

이제 이 둘의 차이를 최소화하는 것에 집중하면 뉴럴 네트워크를 올바르게 학습시킬 수 있습니다. 이 둘의 차이를 손실 함수(Loss function)이라고 하며, 우리는 손실 함수의 값이 최소가 되도록 하는 것을 목표로 합니다.

이때 수많은 선 중 하나의 선을 A라고 할 때, A의 값을 잘 바꾸면 손실 함수를 작아지게 할 수 있습니다. 그러기 위해서는 A 값의 변화와 손실 함수 값 사이에 어떤 관계가 있는지를 알아내야 합니다. A 값의 변화에 따라 손실 함수가 커질 수도 있고 작아질 수도 있습니다. 이 정보는 미분 계산을 통해 가능합니다.

이렇게 얻어낸 정보를 바탕으로 A 값을 손실 함수가 줄어드는 방향으로 수정하는 것이 역전파 알고리즘의 아이디어 입니다.

이러한 역전파 알고리즘을 A, B, C 등의 신경망 내의 모든 선들에 대해 사용합니다. 또 데이터셋에 있는 다른 사진들에 대해서도 같은 과정을 반복합니다. 이미지를 넣어서 손실 함수를 계산하고, 미분 계산을 거쳐, 선들의 값을 변경하는 과정을 계속 반복하는 것입니다.

그러한 과정을 계속 반복하면, 어느 순간 잘못된 값을 내보내던 네트워크는 역전파 알고리즘을 반복함에 따라 손실 함수의 값이 함수의 최소값에 다다르게 되고 최종적으로 올바른 동작을 할 수 있는 네트워크가 됩니다.

---

Appendix. 역전파 알고리즘 (BackPropagarion의 수학적 원리 가볍게 설명)

역전파 알고리즘을 조금 더 심층적으로 살펴보겠습니다. 역전파 알고리즘은 input과 output을 알고있는 상태(=supervised learning)에서 신경망을 학습시키는 방법입니다. 역전파가 사용되는 딥러닝은 MLP(multi-layer perceptron, 다층 신경망)이론의 일종으로 다음과 같은 MLP의 특징을 공유합니다.

1. 초기 가중치, Weight 값은 랜덤으로 주어진다. (이를 Ground Truth 라고 합니다)
2. 각각의 노드(동그라미)는 하나의 퍼셉트론으로 생각할 수 있다. 즉 노드를 지나칠 때마다 활성함수를 적용하게 된다. 활성함수를 적용하기 이전을 Net 이후를 Out이라고 한다면, 다음 레이어의 계산은 Out 값을 사용하게 되며, 마지막 Out이 최종적인 output이 된다.
3. 활성함수는 시그모이드 함수로 한다. 주로 미분의 용이성으로 인해 자주 사용된다. 

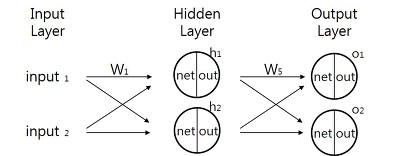
우리가 결과 값으로 얻기를 바라는 값이 Target, 실제로 얻게된 값이 Output이라고 하며 오차 E는 다음과 같이 계산됩니다.

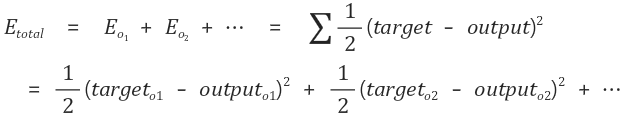
이때의 합의 의미는 모든 output에서 발생한 모든 오차를 더해주는 것입니다. 최종 목적은 이 오차에 관한 E의 함수(Loss Function) 값을 0에 근사시키는 것이며, 오차가 0에 가까워지면 신경망은 학습에 사용된 input들과 그에 유사한 input에 대해서 우리가 원하는 output 정답이라고 할 수 있는 값들을 산출할 것입니다.

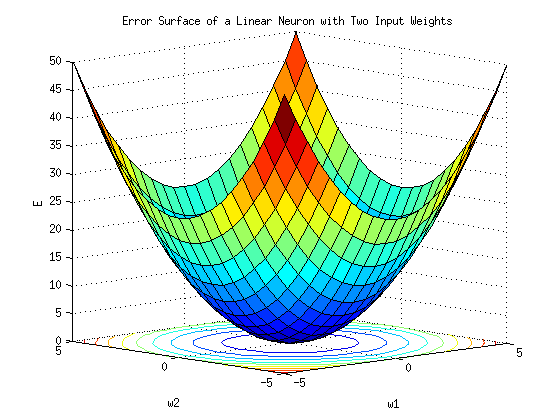
오차 E를 모든 가중치 W1 ... Wn에 대한 방정식으로 본다면 우리가 해야하는 일은 가중치 w를 수정하여 E가 최소가 될 수 있도록 하는 것입니다. 이를 위해 사용하는 것이 경사 감소법(gradient descent)라는 최적화 알고리즘입니다. 기본원리는 기울기가 낮은 쪽으로 연속적으로 이동시켜 값이 최소가 되는 점(극값)에 다다르도록 하는 것입니다.

알고리즘 자체는 단순한데, 총 4단계 정도로 세분화가 가능합니다.

1. 기존에 설정되어 있는 가중치를 사용해서 net, out을 계산합니다. (forward pass)
2. 전체 오차를 각 가중치로 편미분한 값을 기존 가중치에서 빼줍니다.
3. 모든 가중치에 대해서 2를 실행합니다. (output에 가까운 쪽에서 먼 쪽으로)
4. 1~3을 학습 횟수만큼 반복합니다.

이때 output에서 가까운 쪽에서부터 갱신하는 이유는 가까운 쪽에서 사용한 값을 먼 쪽의 계산과정에서 다시 사용하기 때문입니다.

여기까지해서 역전파의 수학적 원리에 대해서도 가볍게 알아보았습니다. 편미분 과정을 포함하여 본격적인 수식 전개는 추후 올라오는 글에서 다시 다루도록 하겠습니다.